One of the salient features at the Computational Multiphysics Laboratory is the ability to simulate large scale two-phase fluid-structure interaction problems. These problems consist of deforming fluid-structure boundaries as well as evolving two-phase fluid-fluid boundary.
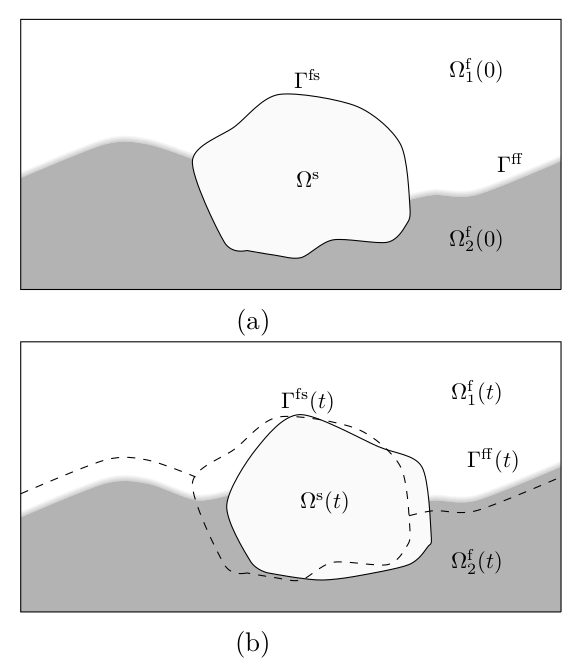
Fig 1. Two-phase fluid-structure interaction schematic: Two-phase fluid and structural domains at the (a) initial ; and (b) deformed configurations.
As can be observed from Fig 1, the objective of the problem is to track the deforming fluid-structure interface while evolving the two-phase fluid-fluid interface and satisfying the equilibrium conditions at the interfaces. We utilize the variational finite element framework in achieving this objective.
The fluid-structure coupling has been depicted in Fig 2, where we solve the incompressible Navier-Stokes equations in three-dimensions on the fluid domain and multibody structural equations in the structural domain. Here, sf denotes the surface tension force in the Navier-Stokes equations. The velocity continuity and force equilibrium are satisfied at the fluid-structure interface. To tackle the issue of instability in small structure-to-fluid mass ratio regimes, a nonlinear iterative force correction technique is employed [1].
Apart from the fluid-structure interaction, the fluid-fluid interface is evolved with the help of the conservative phase-field Allen-Cahn equation [2] and the turbulence is modeled using hybrid RANS/LES [3] (shown in Fig 3).
This fully coupled two-phase fluid-structure formulation has been extensively validated [4] and utilized to demonstrate large scale applications in offshore and marine engineering dealing with drillship-riser system (Fig 4).

Fig 2. Three-dimensional coupling between the incompressible Navier-Stokes and multibody structural equation.
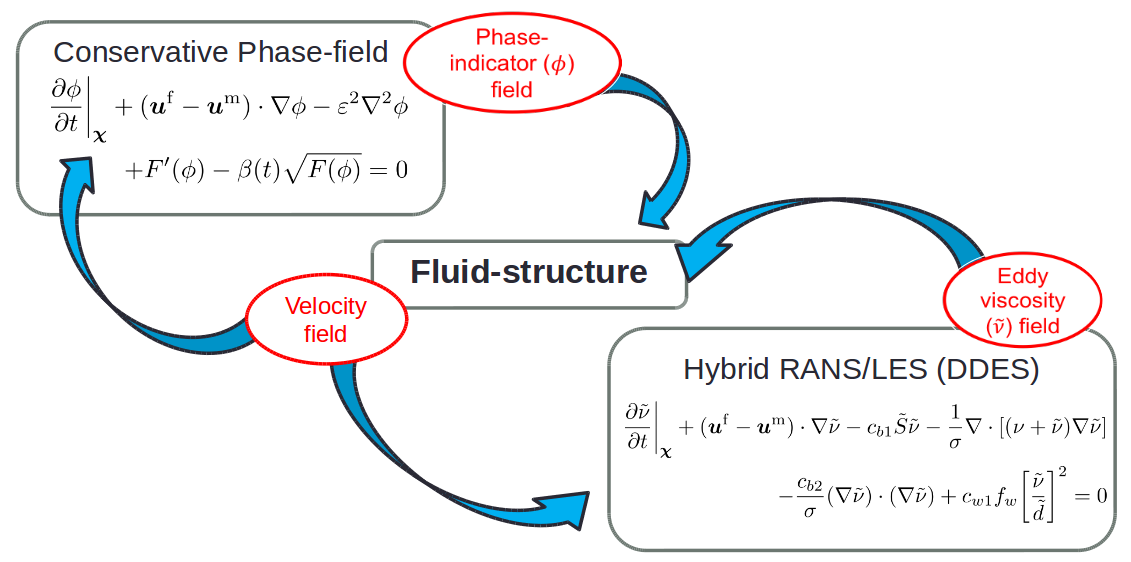
Fig 3. Three-dimensional coupling of the phase-field Allen-Cahn and hybrid RANS/LES turbulence equations with the fluid-structure framework.
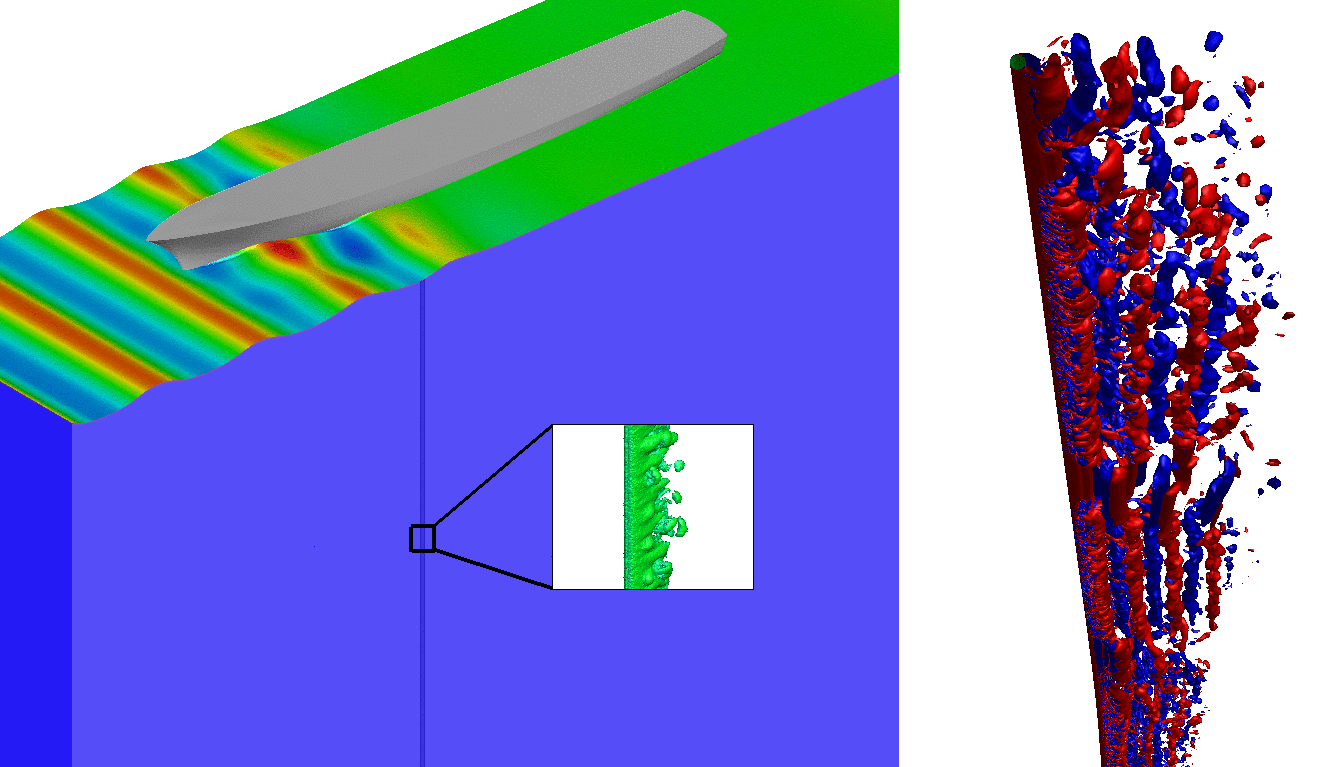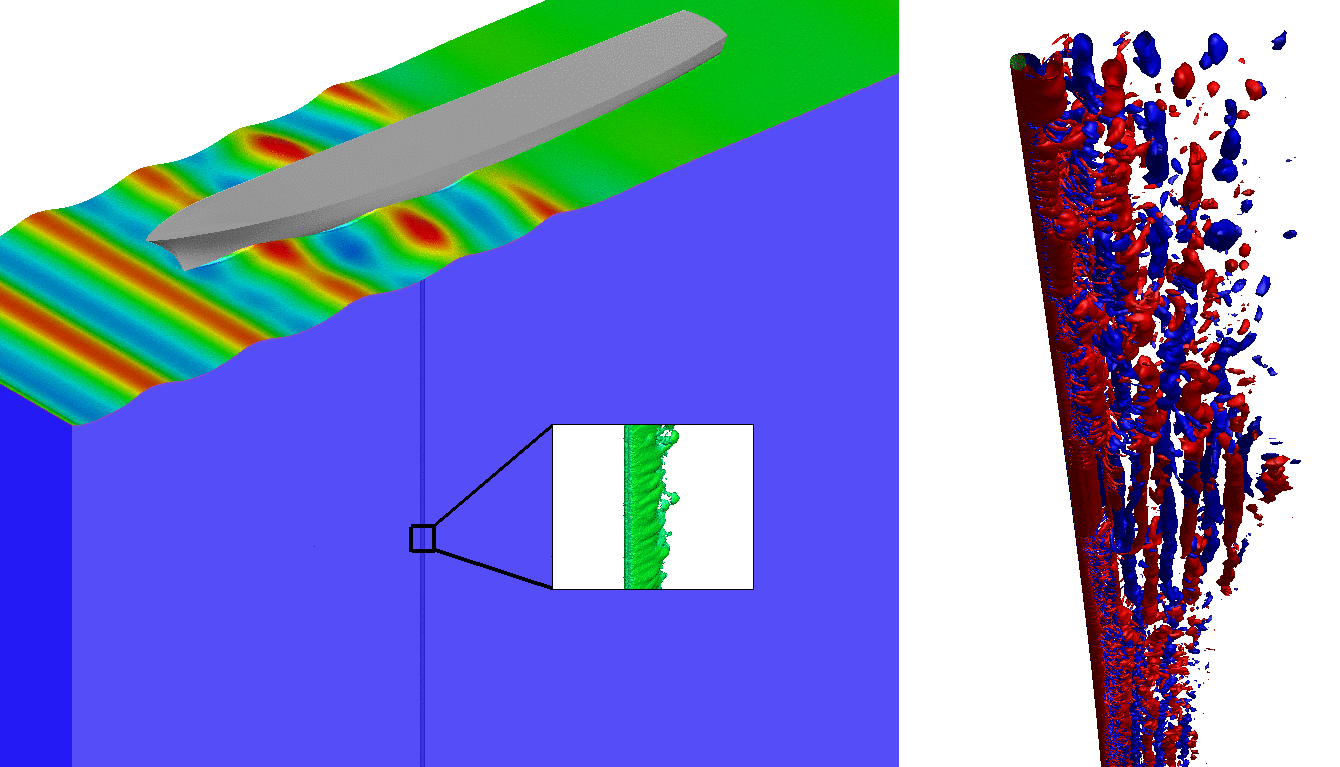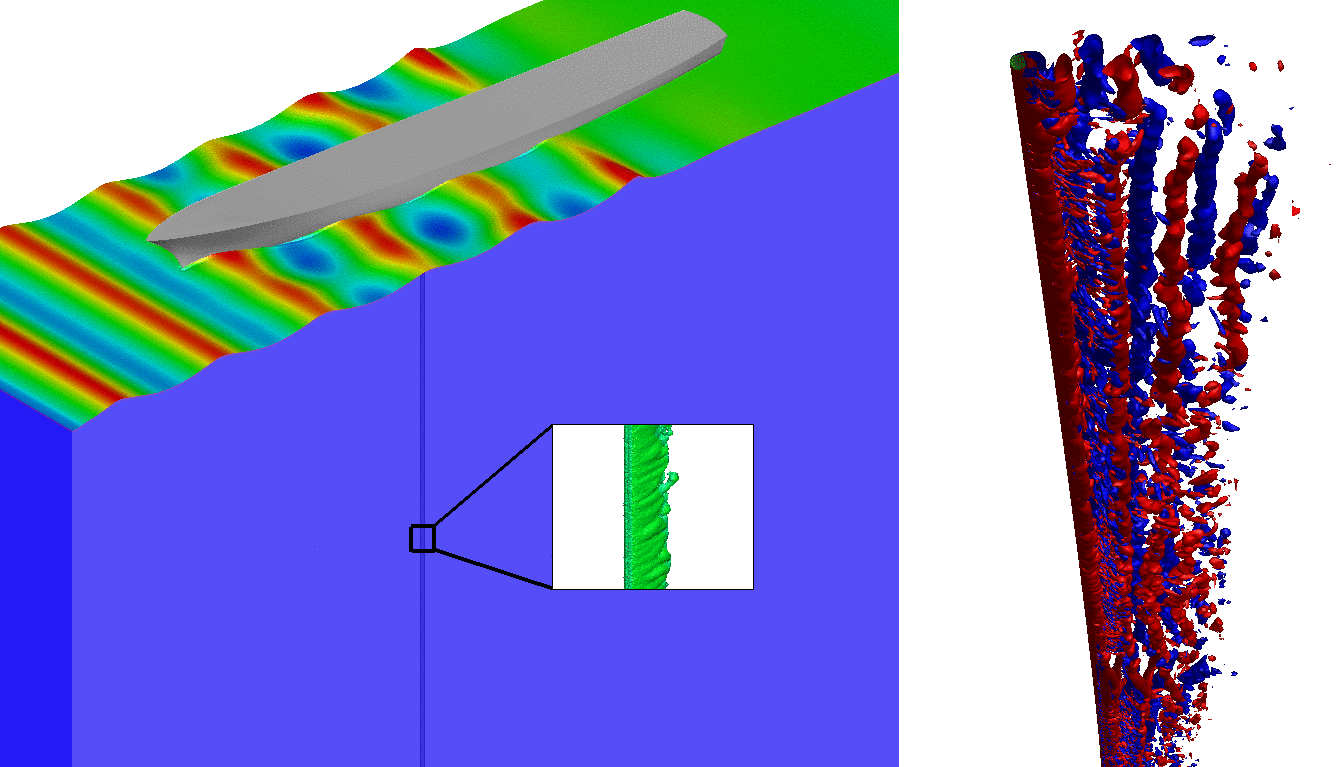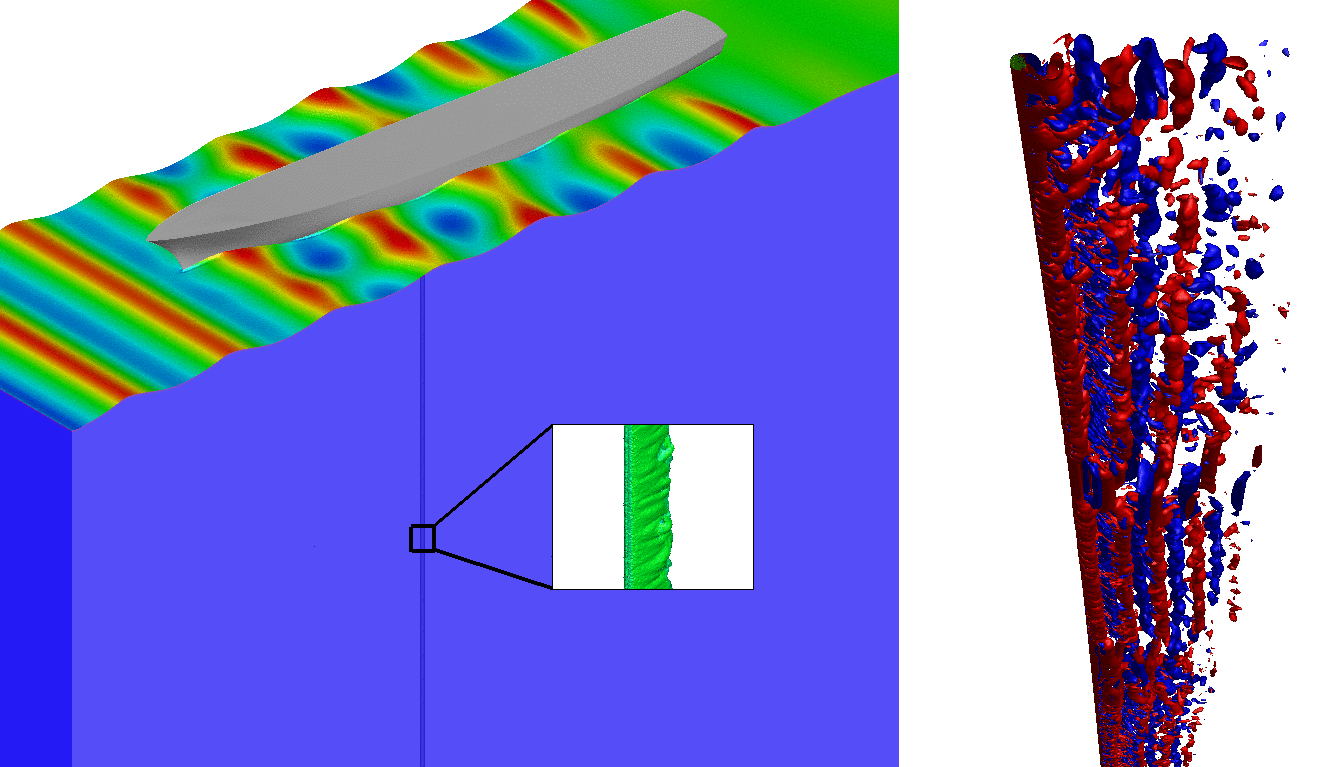
Fig 4. Coupled marine drillship-riser system.
References
[1] Jaiman RK, Pillalamarri NR, Guan MZ, A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow, Computer Methods in Applied Mechanics and Engineering, 301:187-215 (2016).
[2] Joshi V, Jaiman RK, A positivity preserving and conservative variational scheme for phase-field modeling of two-phase flows, Journal of Computational Physics, 360:137-166 (2018).
[3] Joshi V, Jaiman RK, A variationally bounded scheme for delayed detached eddy simulation: Application to vortex-induced vibration of offshore riser, Computers and Fluids, 157: 84-111 (2017).
[4] Joshi V, Jaiman RK, A hybrid variational Allen-Cahn/ALE scheme for the coupled analysis of two-phase fluid-structure interaction, International Journal for Numerical Methods in Engineering, 117(4), 405-429 (2019).